√100以上 三 平方 の 定理 応用 168539

四平方の定理 ~三平方の定理の拡張~四平方の定理三平方の定理というと, 直角三角形において,(斜辺の2乗) = (他の2辺の2乗の和)が成り立つという有名な定理ですここでは, 三平方の定理(平面上の定理)を3次元に拡張した, 四三 平方 の 定理 三平方の定理 中 3 数学 三 平方 の 定理 現在小6生のみ小5・3月号以前に＜チャレンジタッチ＞を受講されたことのある場合、1月号教材とあわせて、進研ゼミ専用タブレット「チャレンジパッド2」をお届けします。四平方定理) ラグランジュの四平方定理は，定理の名前は同じですが，全く違う内容の定理です． 定理 全ての自然数は，高々 4 個の平方数の和で

三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ

三 平方 の 定理 応用

三 平方 の 定理 応用-Nov 28, 16三平方の定理（ピタゴラスの定理）を使えば求められるんだ。 DFの長さをxcmとして、三平方の定理（ピタゴラスの定理）に代入してみると、 13²三平方の定理 例題 三平方の定理 三平方の定理2 三平方_平行四辺形の対角線 特別な直角三角形_補助線が必要な問題 二等辺三角形の面積 台形の面積 三平方_三辺の長さから三角形の面積を求める 三平方_座標平面の三角形 三平方_座標(最短距離) 三平方_座標(点と直線の距離) 三平方_折り返し

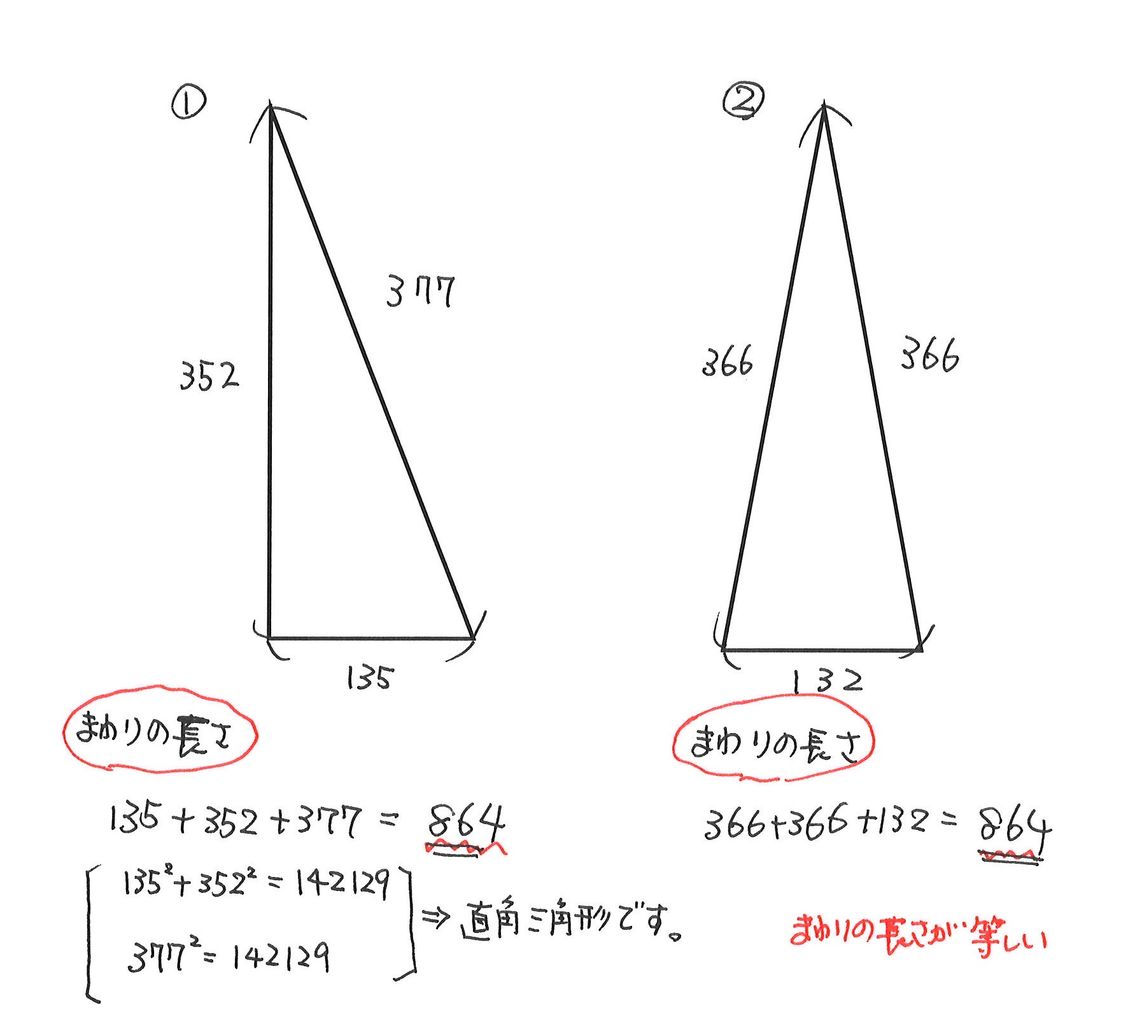
三角形のペア 大田 桐光本部校 ブログ

三平方の定理の応用問題中学3年数学 28三平方の定理と空間図形（1） 直方体の対角線の長さの求め方中学3年数学 立体の切り口の面積中学3年数学 正四角錐と三平方の定理中学3年数学 円錐と三平方の定理中学3年数学May 04, 17ラグランジュ (Lagrange) の四平方定理 以前，三平方の定理の拡張である四平方の定理を紹介しました． (–>Apr 14, 21三 平方 の 定理 高校 入試 難問 図形問題解決のために知っておくべき三平方定理の証明方法 中学数学 理科 寺子屋塾の復習サイト 中学数学発展 シンプルだけど難しい ラ サールの難問 平面図形 定期テストや高校入試に レオンの中学数学探検所三 平方 の 定理 高校 入試 難問

三平方の定理とは、別名「ピタゴラスの定理」とも呼ばれる、とても古くからある数学の定理です。 具体的にはCを直角とする直角三角形ABCの辺 a,b,c a, b, c について、 a2 b2 = c2 a 2 b 2 = c 2結晶構造の探究 ･･････ 金児 正史Oct 10, 19三平方の定理（ピタゴラスの定理）の応用問題パターン10選 三平方の定理（ピタゴラスの定理）は、直角三角形において成り立つ定理です。 また、どんな定理だったかと言うと、$3$ 辺の長さについての定理でした。

三平方の定理とは？ / 三平方の定理の逆 / 有名角と比 / 2点間の距離 / 円の中心と弦との距離 / 空間図形の対角線・高さ / 空間図形とひもの最短距離68 = ±2√17 = ±4 三平方の定理の応用問題 5 底面の半径が 2 cm，母線の長さが 8 cm の円錐について，次の問いに 答えよ。 ⑴ 側面の展開図のおうぎ形の中心角を求めよ。 ⑵ 右の図のように，円錐の側面上をまわるように，点 A から点 A ま でひもをかける。

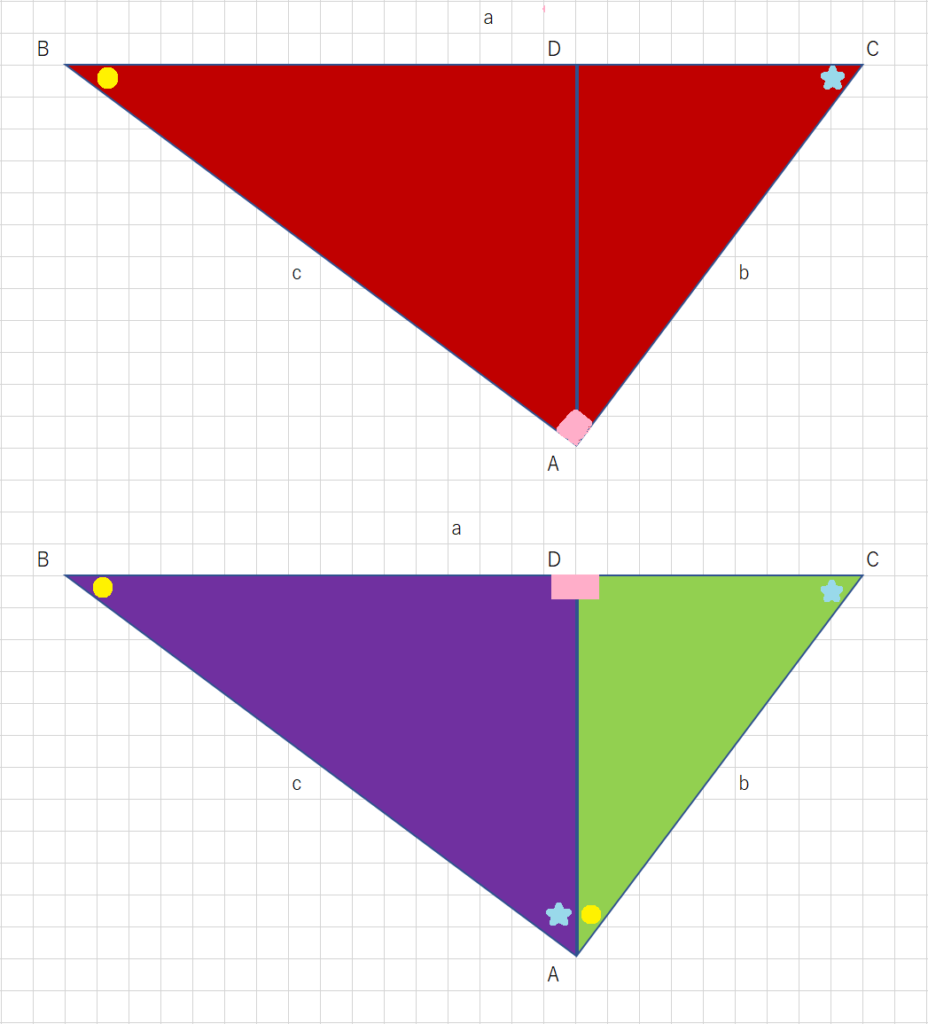
中学数学 直角三角形の三平方の定理とは ピタゴラス 平方根 の定理をexcelの図形で Curlpingの幸せblog

高校数学 3辺の長さが等しい 三脚型 四面体の体積 受験の月

Apr 04, 19右下の三角形を見てもらえばわかる通り、正六角形の各頂点から中心に線を引くと三角形ができて、それはすべての角が60°になるから、正三角形だね！ 正三角形ということは、すべての辺の長さが等しい。 つまり、下図のようになるよ！ ということは、各頂点から点Pまでの長さが 6 6 だから、三平方の定理を用いると、 x2 = 62 –22 x 2 = 6 2 – 2 2 ∴ x2 = 36− 4 = 32 x 2中文名 勒让德定理 外文名 Legendre's formula 提出者 勒让德 应用学科 数学 适用领域范围 代数三平方の定理　 (ピタゴラスの定理) c2= a2 b2

灘中算数17二日目4番 解説速報 算数ソムリエブログ 中学受験突破のために

三角形のペア 大田 桐光本部校 ブログ

テトラパックと空間充填 ･･････ 小森 弘三;平面図形への応用 平面図形への応用 1辺 の長さが 1cm の正方形の対角線の長さを求めてみよう。 対角線の長さを xcm として、三平方の定理を使って求め るよ。 対角線の長さを xcm とすると、 三平方の定理から x 2 ＝ 1 2 ＋1 2三平方の定理(基本問題1) 例題 次の直角三角形で、xの値を求める。 x 2 6 xが斜辺なので 2 2 6 2 = x 2 x 2 = 40 x = ±2 √ 10 x >

高校数学 立体 正四面体 直円錐 表面上の最短経路 受験の月

中3 数学 三平方の定理 中学生 数学のノート Clear

May 10, 21三 平方 の 定理 応用 三 平方 の 定理 応用 解き方 三平方の定理とは、直角三角形において 斜辺の長さの2乗は、他の辺の長さの2乗の和に等しくなる。 というものです。 文章だけでは、難しく見えますが 非常に単純な定理です。 数学史から入る「三平方の定理」 「三平方の定理」は，いつ，どのようにして発見されたか ･･････ 片野 善一郎正解率 \ (02 17 この問題では、当然 x x は正の値なので x = 2√17 x = 2 17最高 Ever 三 平方 の 定理 応用 中3数学応用 空間図形と三平方の定理の練習問題 三平方の定理の応用 Studydoctor三平方の定理の応用問題 中学3年数学 Studydoctor 中3数学 三平方の定理の応用 折り曲げ 2 Youtubeの活用， 平方根の計算などを基礎的・基本的な内容して活用していく．また，発表する機会

折り返した図形の角度を求める2つのコツ Qikeru 学びを楽しくわかりやすく

三平方の定理 の問題のわからないを5分で解決 映像授業のtry It トライイット

平方根 平方根(1) 問題一括 (8,085Kb) 解答一括 (9,324Kb) 平方根(2) 平方根の大小 有理数と無理数 平方根の乗法 平方根の除法 平方根の性質(1) 平方根の性質(2) 平方根の近似値 根号を含む計算 有理化 平方根の加法・減法(1) 平方根の加法・減法(2) 平方根の解答 下の図のように補助線をひき、左の直角三角形に 三平方の定理を用います。 x2 = 22 x 2 = 2 2 8 2 x2 = 68 x 2 = 68 x = ±√68 x = ±Dec 07, また、三平方の定理が成り立つ三辺の比の中で、平方根（ルート）が含まれるものでは、次の⑤と⑥が有名。 直角三角形の問題の中では、一番テストで使う確率が高いものです。

無料 中３数学 発展 応用問題 問題プリント 333 三平方の定理１

國三 Junior High数学的 数学 三平方の定理 筆記 Clear

やまぐち学習支援プログラム 領 域 番号 学習プリントについて プリント 中3数学 00 やまぐちっ子学習プリント教科書対応表（中学校3年数学）直角三角形においては三平方の定理が成り立つため，3つの角が30°，60°，90°である直角三角形と，45°，45°，90°である直角三角形の3辺の長さには，それぞれ次のような関係が成り立っています。 特別な直角三角形の3辺の比 30°，60°，90°の 直角三角形 45°，45°，90°の 直角三角形 3辺の比は となります。 3辺の比は中学校3年生数学 WEB問題（チャレンジシート） 中学校3年生 数学科 ①式の展開と因数分解 問題 解答 ②平方根 ① 問題 解答

中3数学 空間図形の対角線 高さ 練習編 映像授業のtry It トライイット

1 Adb De Lihat Cara Penyelesaian Di Qanda

スペースシャトルの速度をピタゴラスの定理で測る ･･････ 楳木 敏之;無料 中2数学 応用 発展問題 問題プリント 333 三平方の定理1 三 平方 の 定理 証明 中学生 三 平方 の 定理 証明 中学生中線定理とは 中線定理とは、図の abcにおいて辺bcの中点をmとするとき、 であるというものでした。三平方の定理 例題 三平方の定理 三平方の定理2 三平方_平行四辺形の対角線 特別な直角三角形_補助線が必要な問題 二等辺三角形の面積 台形の面積 三平方_三辺の長さから三角形の面積を求める 三平方_座標平面の三角形 三平方_座標(最短距離) 三平方_座標(点と直線の距離) 三平方_折り返し

Rjemtf8izznzlm

無料 中３数学 発展 応用問題 問題プリント 334 三平方の定理２

Jan 10, 18三平方の定理を利用して四角すい、円すいの体積を求める問題です。 まずは基本的な円錐、正四角錐の体積の求め方をしっかり確認してから、いろいろな応用問題を解くようにしてください。 円錐の体積 下のような底面積の半径が6cm、 17年2月14日Dec 17, 18三平方の定理の平面図形の応用問題です。入試にもよく出題される問題をアップしていきます。定期テスト対策、高校入試対策の問題として利用してください。学習のポイント 今までの図形の知識が必要となる問題が多くなります。三 平方 の 定理 直角 三角形 Pictngamukjp5mhn 直角三角形において、「直角」をはさむ2つの辺の長さを \ (a,b\)、斜辺の長さを \ (c\) としたとき 三平方の定理（ピタゴラスの定理）と公式の証明忍者が用いた三角の知恵｜アタリマエ!3

ある三平方の定理の証明方法 中学校程度の数学で理解しよう 身勝手な主張

國三 Junior High数学的 数学 三平方の定理 筆記 Clear

Sep 02, ピタゴラスの定理を応用した「三角測量の原理」を用いることで、地球と星までの距離を計測することも可能。 地球は太陽のまわりを公転しているので、夏と冬に同じ星を観測すれば、地球と太陽の間の距離の2倍離れた位置から同じ星を見たことになります。三角形の見分け方 ABCにおいて辺の長さを小さい順に a,b,c とすると a^2b^2>c^2 ならば ABCは 鋭角三角形 a^2b^2=c^2 ならば ABCは 直角三角形 a^2b^2<c^2 ならば ABCは 鈍角三角形 この特徴を覚えておけば 次のような問題を解くことができるようになります。「三平方の定理の利用」の授業 母線の長さが同じでも ･･････ 伊藤 勇治;

ほう べき の 定理

中３数学12 三平方の定理４ 空間図形 発展問題プリント 問題 336

三平方の定理は「ピタゴラスの定理」とも呼ばれ、直角三角形の３辺の長さの関係を表す式のことである。 図のように直角三角形の斜辺をc, 他の2辺をa, bとすると c2 = a2 b2の関係が成り立つ。 a b c a b c c 2 = a 2 b 2Nov 07, 18三平方の定理の応用問題 ここまでで、三平方の定理の基礎はだいぶ仕上がってきたと思います。 最後に、少しだけ難易度が上がった応用問題を \(2\) 問解いてみましょう。 応用問題①「1 辺と 1 角から辺の長さを求める」拉格朗日四平方和定理 每个正整数均可表示为四个整数的平方和。 Every positive integer is the sum of four squares 例如： 证明： 可以直接验证如下恒等式 ，其中 由于 1 与 2 都明显满足这个定理，那么只需要考虑大于 2 的正整数。 而这些正整数都可以分解成素数的

二 等辺 三角形 角度 二等辺三角形の底辺は 1分でわかる意味 長さの計算 角度 高さ 三平方の定理との関係

三平方の定理 特別な直角三角形 イ弋マ本ゼミナール

0より x =2 √ 10 x 4 5 斜辺が5なので x 2 4 2 =5 2 x 2 = 2516 x 2 =9 x=±3 x>0より x=3 次の直角三角形で、xの値をそれぞれ求めよ。Mar 07, 21A B C ABC ABC の面積を表します。 三平方の定理の三次元空間バージョンです！ なお，四平方の定理というと整数論におけるラグランジュの四平方和定理（ →整数論の美しい定理7つ の5つ目）のことを指す場合もあるので注意して下さい。 目次 四平方のFeb 12, 17三平方の定理というと, 直角三角形において, (斜辺の2乗) = (他の2辺の2乗の和)

三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ

三平方の定理 3 4 5 三平方の定理を知る Rspmg

三 平方 の 定理 応用 問題 三 平方 の 定理 応用 問題例題1 下の図の、\\(x\\) の値を求めなさい。 解答 下の図のように補助線をひき、左の直角三角形に 三平方の定理を用います。直角三角形ABD について三平方の定理を適用すると 22 (x1)2= (√13nnnnn)2 (x1)2=9 x1=3 (>0) x=2 例2 長方形の向かい合う辺の長さは等しいので，次の図で AH=DC になる． この AH の長さと AB の長さから三角形 ABH について三平方の定理を使うと辺 BH が求まり， HC

三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ

中３数学応用 おうぎ形と三平方の定理の練習問題 中学生勉強サイトあかね先生

中3 中3数学 三平方の定理の利用 中学生 数学のノート Clear

世界が変わる裏技 三平方の定理を５秒で計算するテクニック Youtube

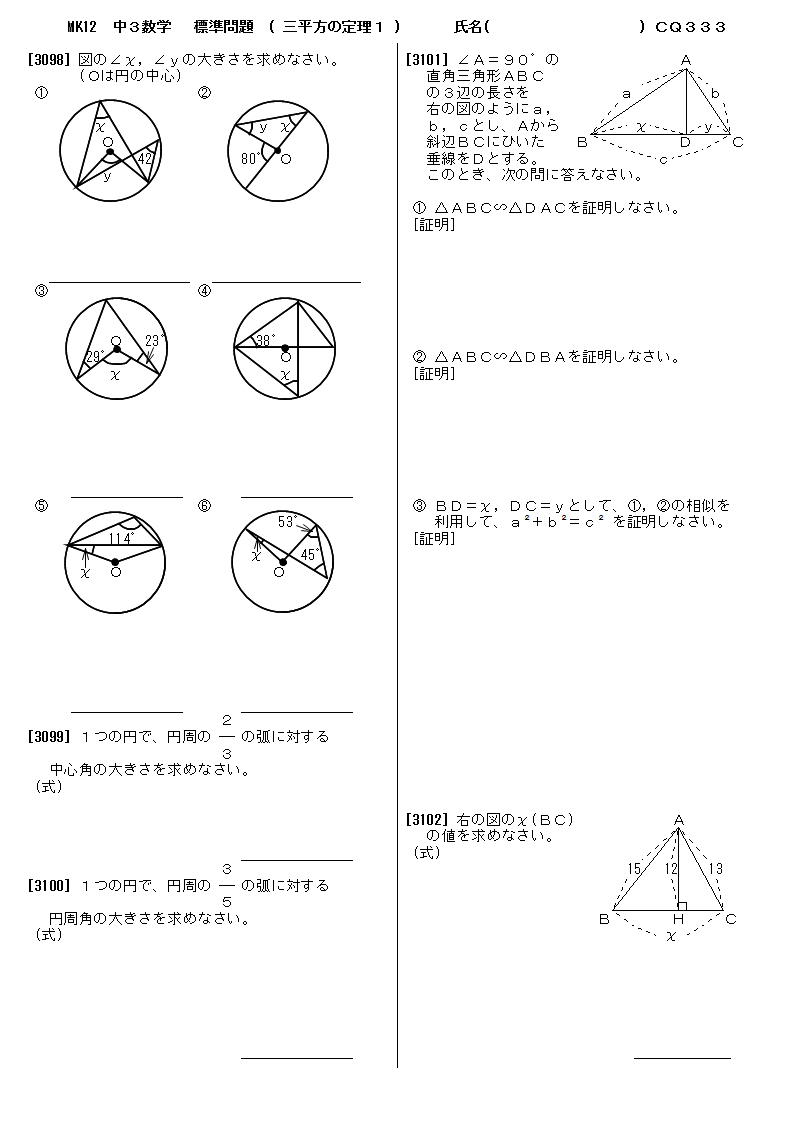
直角 三角形 三 平方 の 定理

中学数学到達度テスト集中３後期 相似な図形 円 三平方の定理 図形と計量 Gakurin1346 学林舎 通販 Yahoo ショッピング

最新三 平方 の 定理 の 証明 最高のぬりえ

三平方の定理 平面図形のいろいろな応用問題 無料で使える中学学習プリント

三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典

三平方の定理 ピタゴラスの定理 と証明 Rikeinvest

三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典

ハンスーの備忘録

改訂版 ４プロセス数学 P84 ８ 空間図形への応用

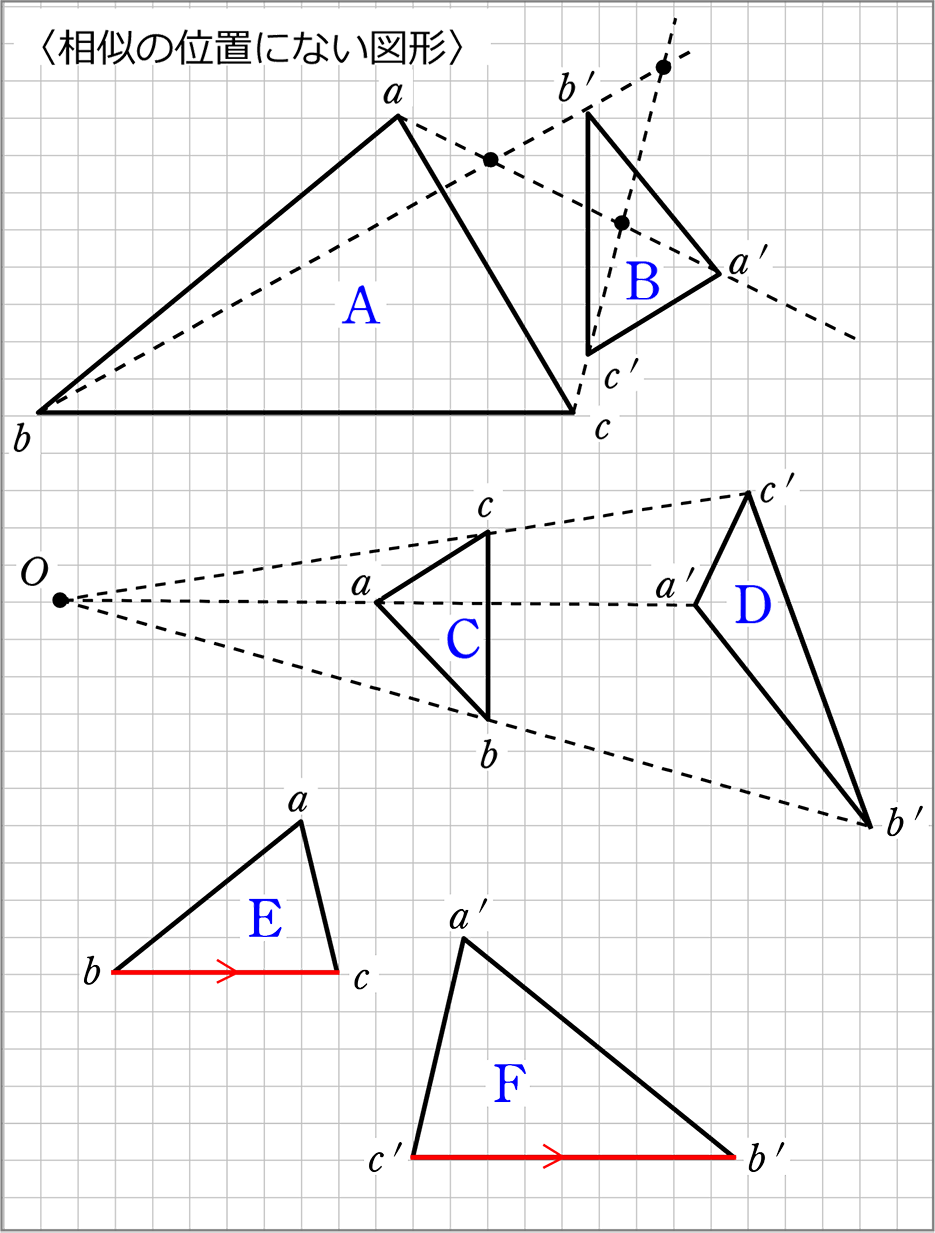
中学数学 図形の相似

Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 高校生なう スタディサプリ進路 高校生に関するニュースを配信

数学 第22回 三平方の定理の応用 高校入試ｃｈｕサポ学力アップ問題集対応15 下野新聞 Soon スーン

三平方の定理と相似の問題 無料で使える中学学習プリント

三平方の定理をパズルで証明 色んなパズルに挑戦してみよう 数学の面白いこと 役に立つことをまとめたサイト

直角 三角形 三 平方 の 定理

数学 中3 70 三平方 空間図形への利用 長さが最小編 Youtube

1 26 三平方の定理の応用だ 神栖市立神栖第二中学校

1 Adb De Descubre Como Resolverlo En Qanda

このab間の距離を求めなさい 図に示すようにabを直径とする半円と そ Okwave

2 Acm m Lihat Cara Penyelesaian Di Qanda

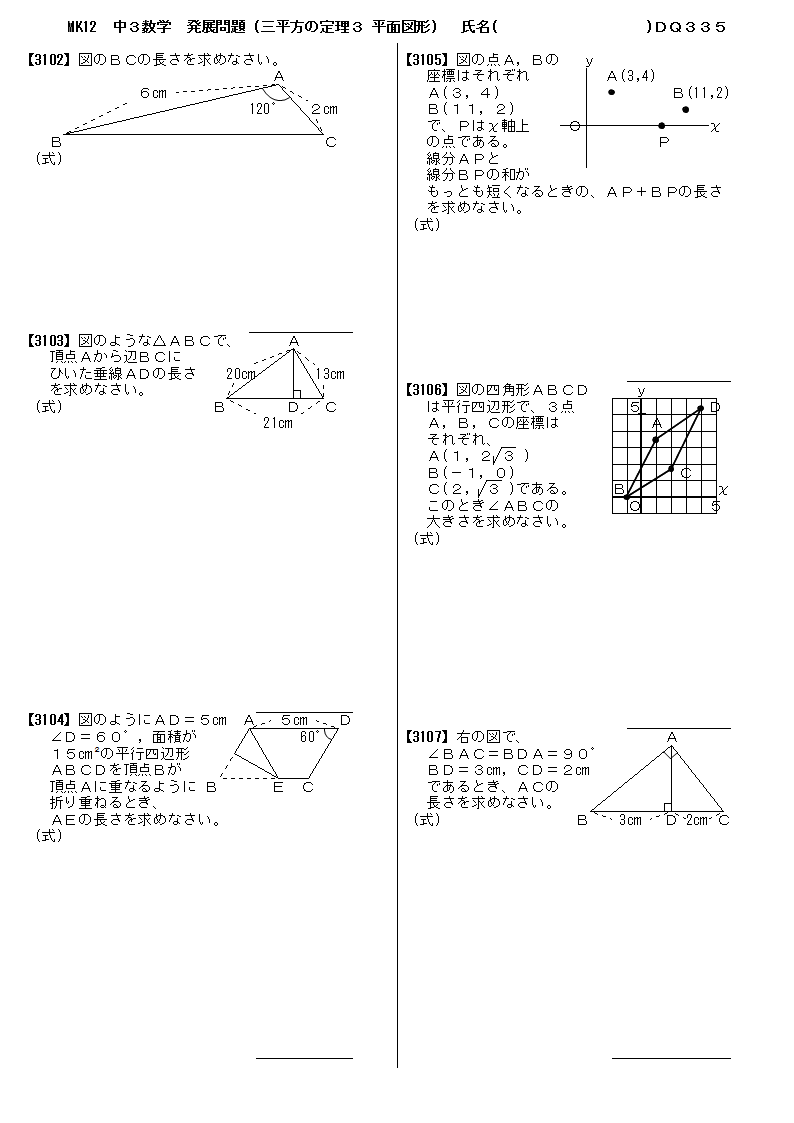
無料 中３数学 発展 応用問題 問題プリント 335 三平方の定理３ 平面図形

三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典

三平方 折り返し

三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典

無料 中３数学 発展 応用問題 解答プリント 336 三平方の定理４ 空間図形

無料 中３数学 発展 応用問題 解答プリント 334 三平方の定理２

改訂版 クリアー数学 P81 27 空間図形への応用

中3 数学 三平方の定理 中学生 数学のノート Clear

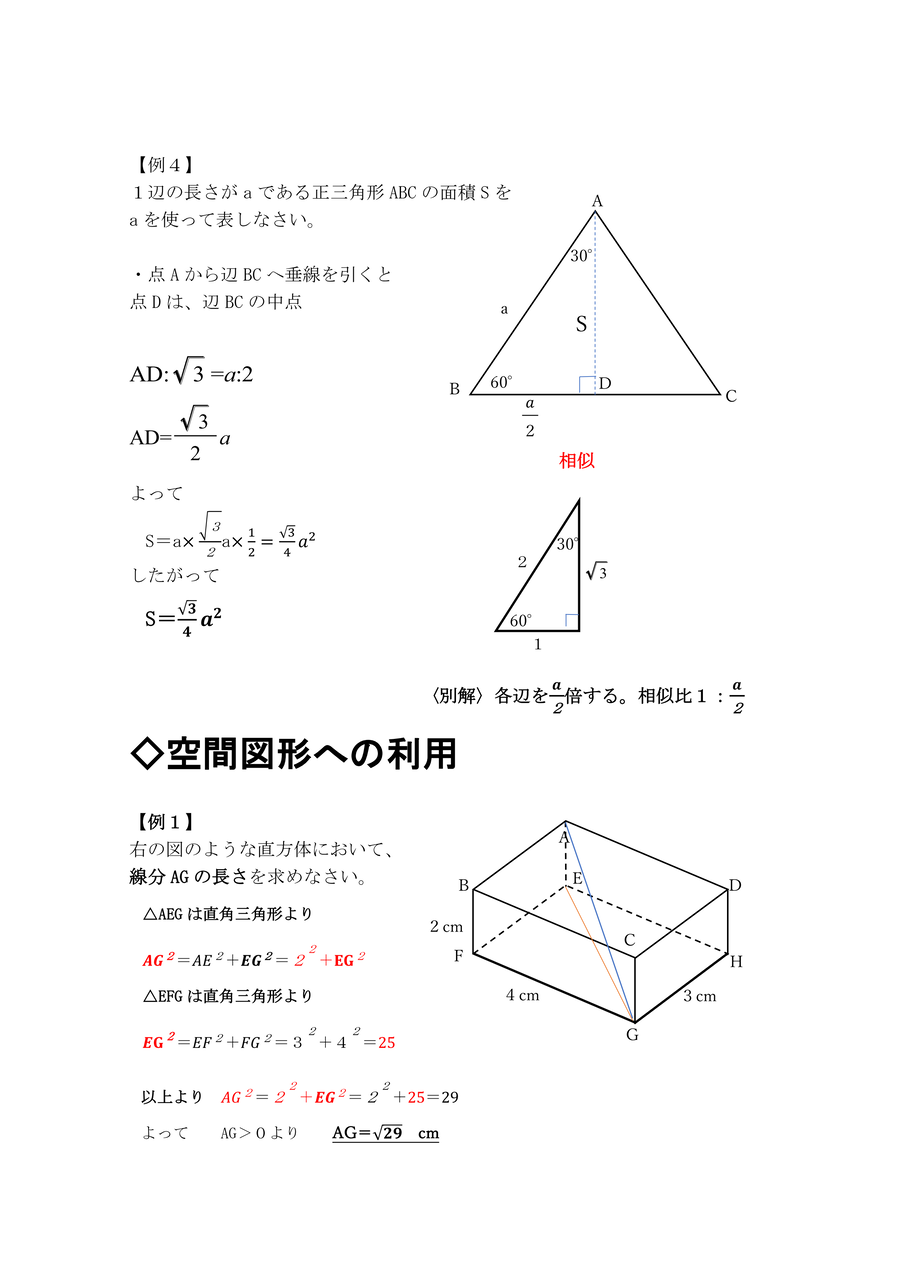
中学校数学 証明のコツ 三平方の定理とは

誰か頭いい人この図形の面積求めてください 解き方が分かりません 計算もわからないで Clear

中3数学 三平方の定理とは 練習編 映像授業のtry It トライイット

平行線と線分の比 辺の長さを求める応用問題４選 教遊者

三平方の定理の適用 ２０１７年度前期日程の奈良教育大学教育学部数学教育専修の入試問題 身勝手な主張

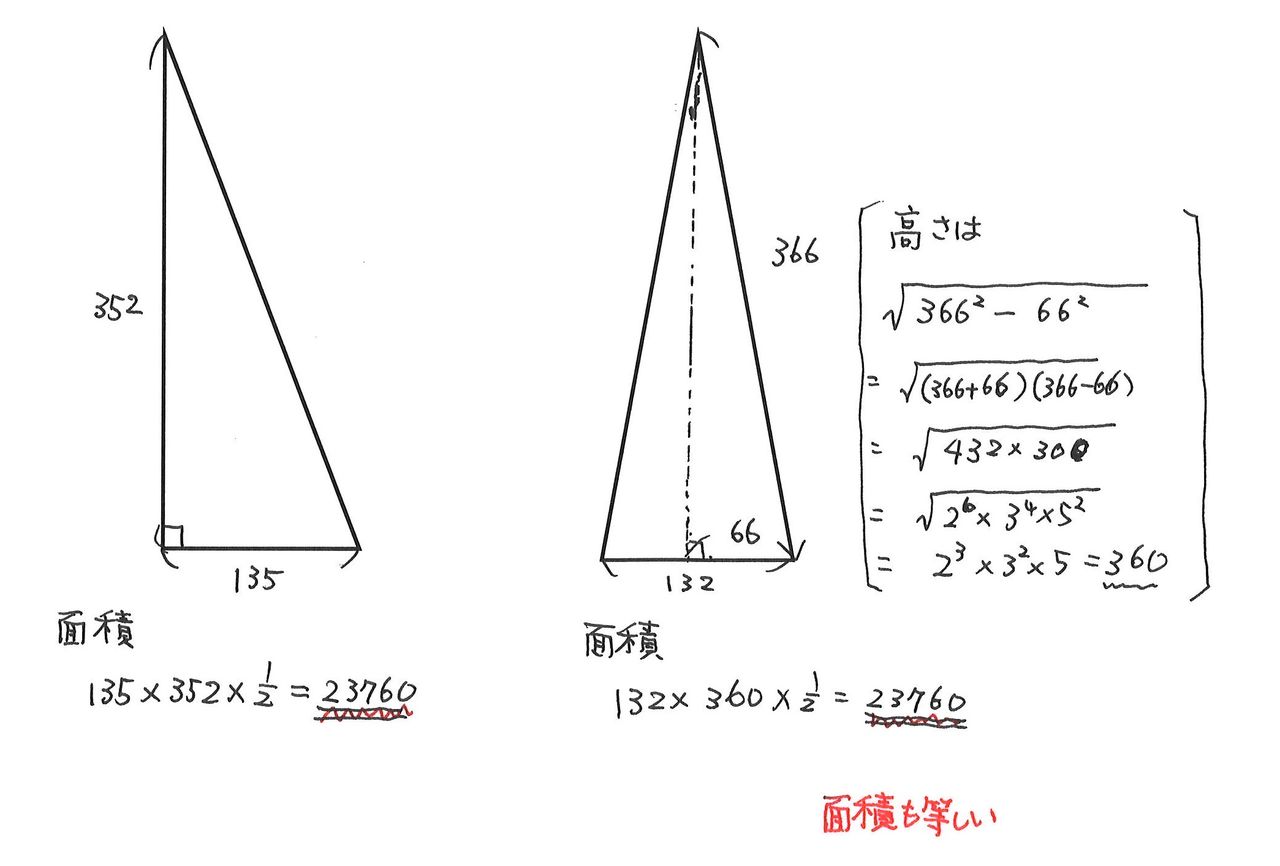
三角形のペア 大田 桐光本部校 ブログ

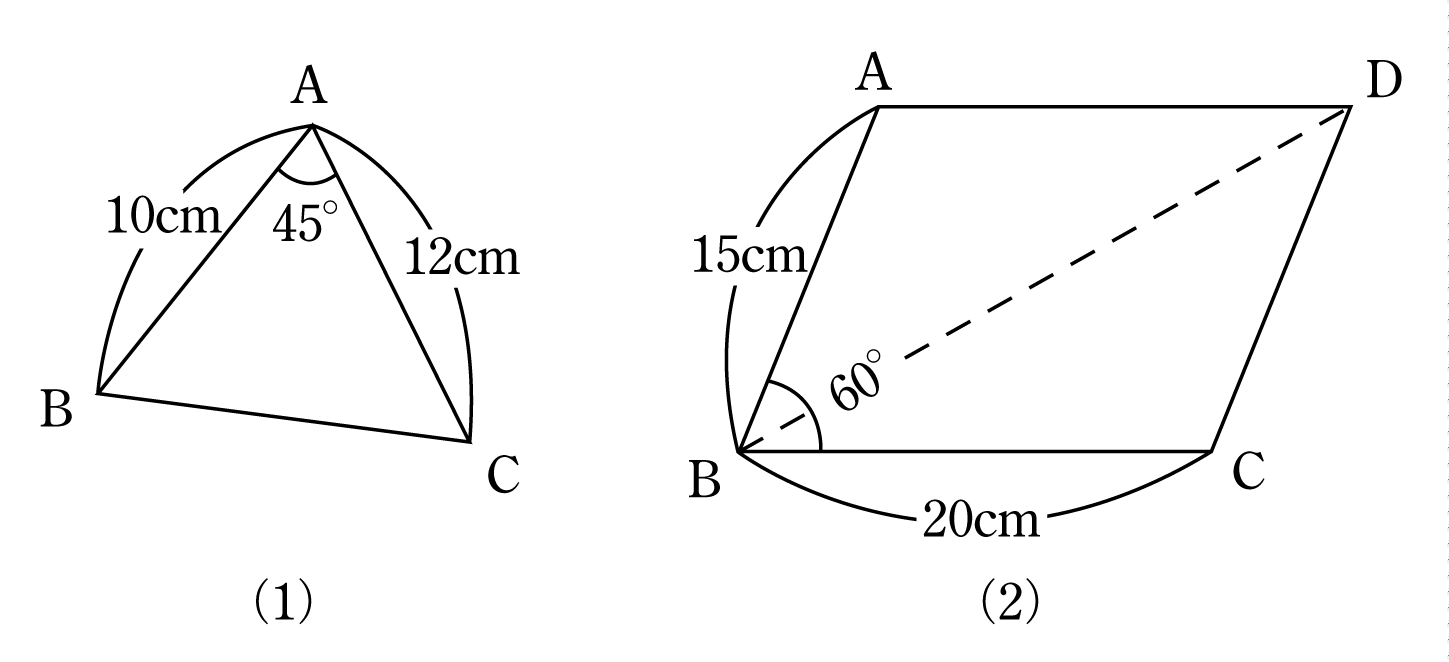
余弦定理と交流ベクトル計算への応用 音声付き電気技術解説講座 公益社団法人 日本電気技術者協会

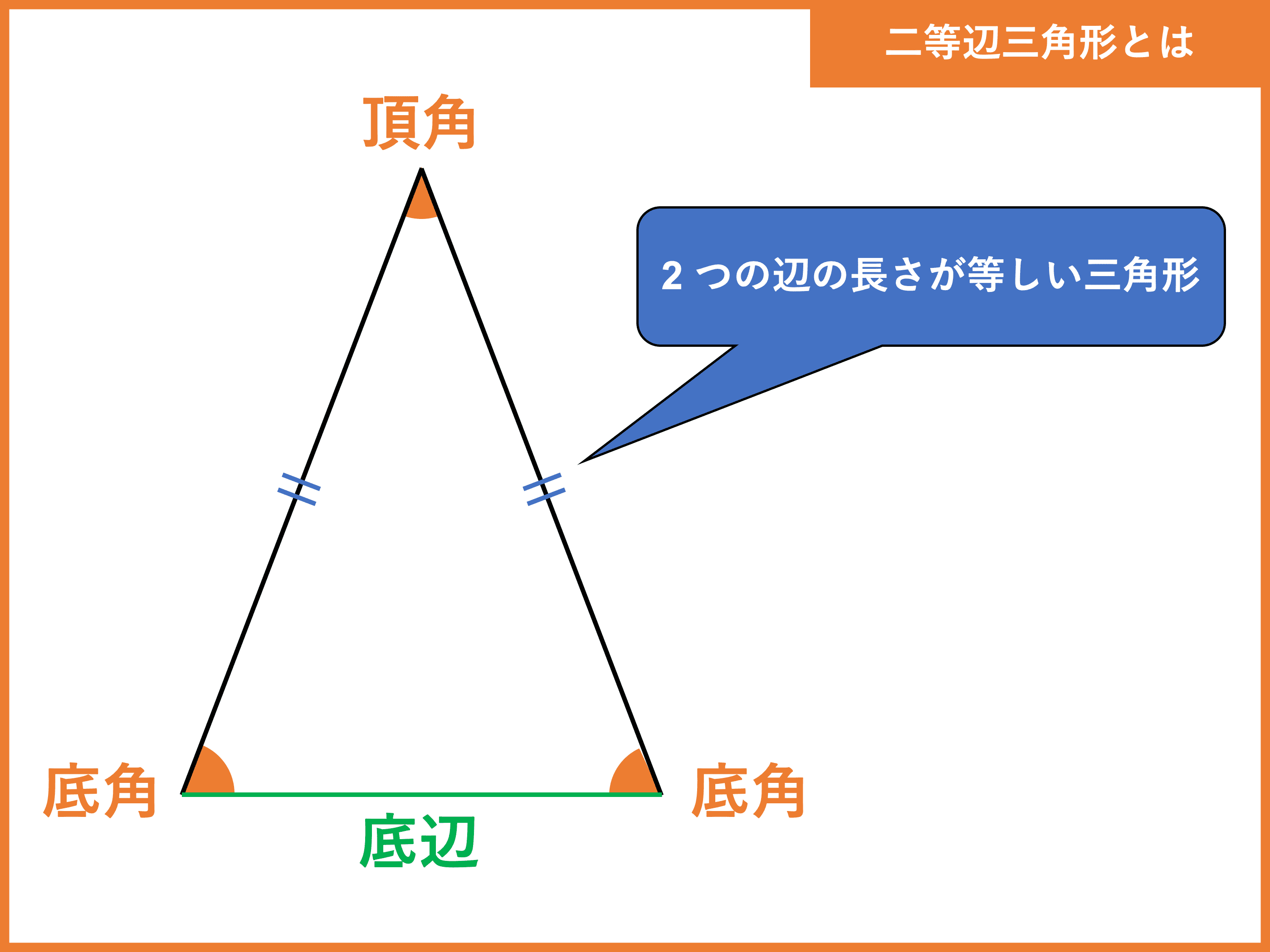
二 等辺 三角形 辺 の 長 さ 三角比 30 45 60 もう一度やり直しの算数 数学

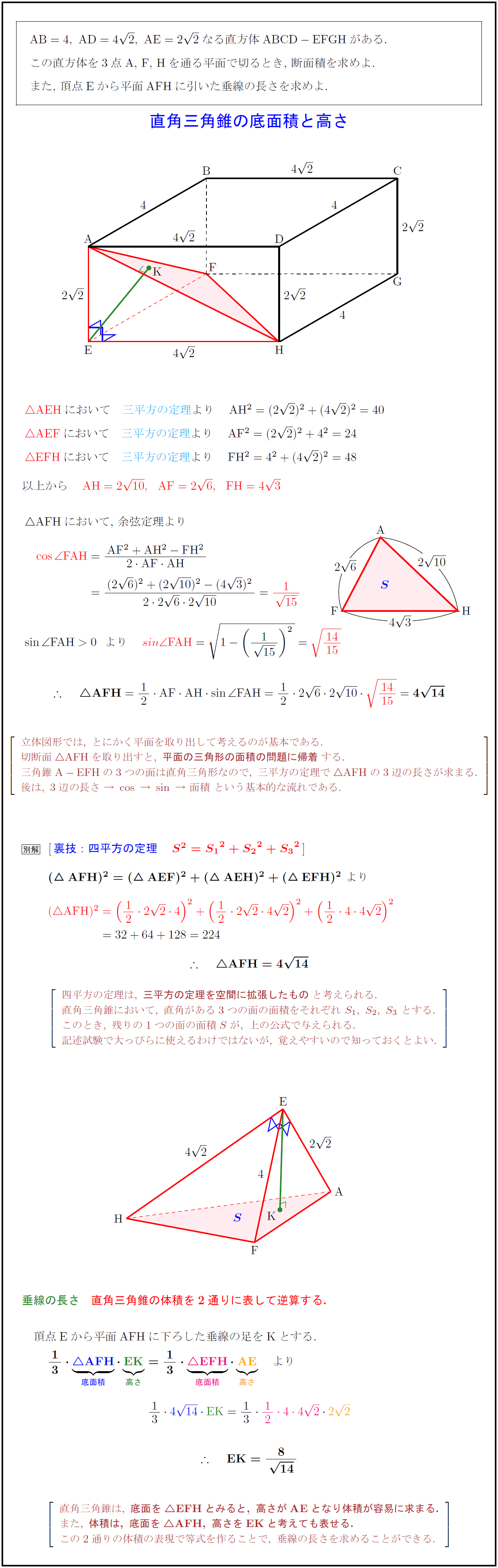
高校数学 直角三角錐 3直角四面体 の底面積と高さ 裏技 四平方の定理 受験の月

三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典

余弦定理 おいしい数学

高校数学 第2余弦定理 三平方の定理の一般化 と第1余弦定理の証明と利用 受験の月

数学 図形問題を得意にする方法 下高井戸校ブログ 中学 高校 大学受験個別指導塾testea テスティー

中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット

高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ

相似 答えは４ ではありません 応用 勉強 Youtube スタディチューブ

三平方の定理をパズルで証明 色んなパズルに挑戦してみよう 数学の面白いこと 役に立つことをまとめたサイト

中学数学 三平方の定理 直角二等辺三角形 オンライン無料塾 ターンナップ Youtube

三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典

ピタゴラスの定理 Wikipedia

三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube

三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典

三平方 三辺の長さから三角形の面積を求める

中3数学 三平方の定理 群馬県渋川市の個別塾 学習塾 ナビ個別指導学院 渋川校ブログ

三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ

3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく

数学 中3 64 三平方 平面図形への利用 面積編 Youtube

余弦定理 おいしい数学

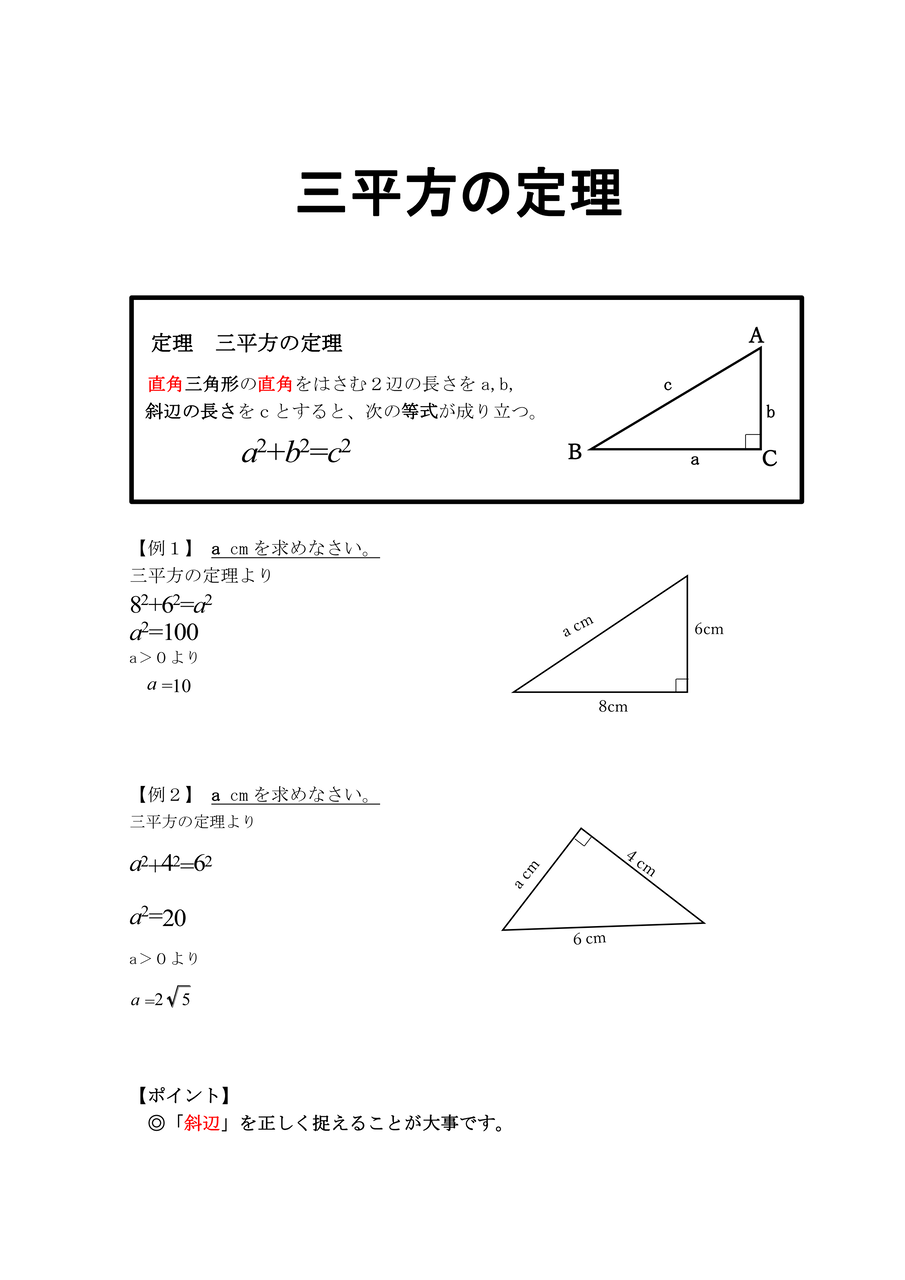
中学校数学 証明のコツ 三平方の定理とは

中学校数学 証明のコツ 三平方の定理とは

三平方の定理の応用 イ弋マ本ゼミナール

いろいろな体積の問題 無料で使える中学学習プリント

中学数学単元別 三平方の定理 数学 中学校 教材 問題集 306 学林舎 通販 Yahoo ショッピング

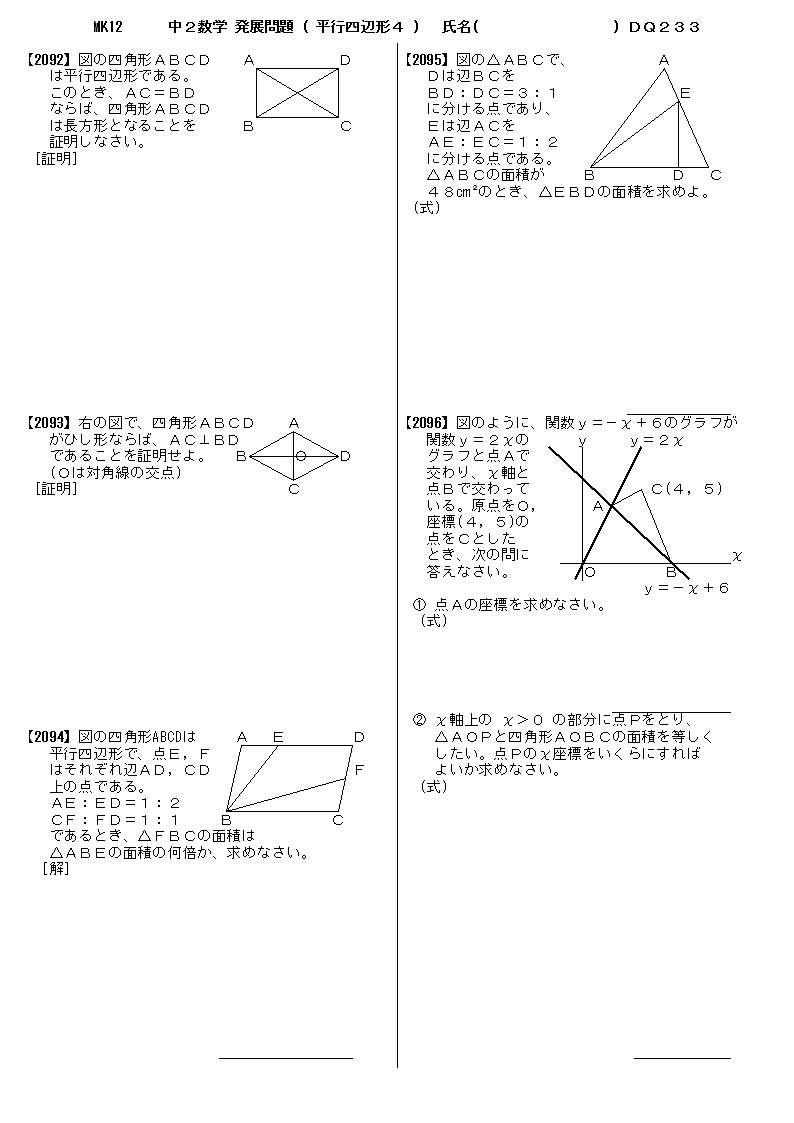
無料 中２数学 応用 発展問題 問題プリント 333 三平方の定理１